How to Keep Your Neighbors Close – in Time
Christoph Lenzen
How to Keep Your Neighbors Close – in Time
Clock synchronization is a central problem in decentralized systems, such as the internet. Here, there are many interconnected computers communicating over large physical distances, and each machine has its own internal clock source. Nonetheless, the system relies upon clock synchronization between computers in the network. How can we synchronize clocks in such a setting, where clocks and message delays are subject to some uncertainty? How closely can clocks be synchronized in such a system, i.e., what is the best system performance that can be achieved? The gradient clock synchronization (GCS) problem seeks to synchronize clocks in a network so as to minimize the clock differences between neighboring nodes in the network.
Clock synchronization is a fundamental problem in computer systems. When designing an algorithm or writing a computer program to solve a particular problem, we typically describe a sequence of steps that a computer should perform in order to solve the problem. We trust that the computer will execute the steps faithfully. In order to do so, the computer relies upon a clock signal in the form of a sequence of electrical pulses. Each pulse of the clock initiates the next step of the computation, and the time between clock pulses should be sufficiently long that the previous step of computation completed before the next pulse. Difficulties arise because we need computers to run quickly and accurately. If the clock pulses are too close together, the computer may not have time to perform the individual steps of the computation, but spacing clock pulses farther apart means that the computer is running slower. The clocks on modern computers run so quickly that even the speed of light becomes a consideration: clock pulses arrive sooner to parts of the computer's circuitry that are closer to the clock source. Thus, different computer components will always be slightly out of sync. It is a subtle art to design computer circuitry that achieves the best synchronization possible and copes with some inherent uncertainty.
The problem of clock synchronization is even more pronounced in decentralized systems, such as the internet. Here, there are many interconnected computers communicating over large physical distances, and each machine has its own internal clock source. Nonetheless, the system relies upon clock synchronization between computers in the network. How can we synchronize clocks in such a setting, where clocks and message delays are subject to some uncertainty? How closely can clocks be synchronized in such a system, i.e., what is the best system performance that can be achieved?
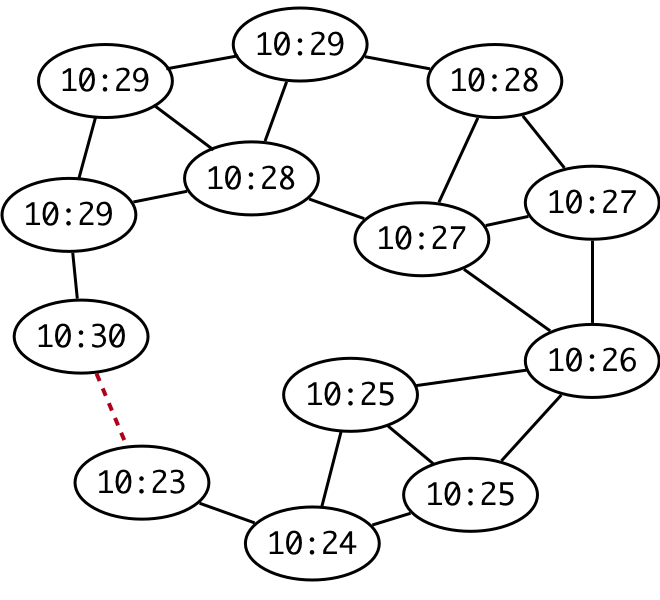
Figure1: A network with clock values. All neighboring clocks differ by at most one minute, except for the neighboring clocks indicated by the dashed line. Our goal is to maintain clock values so that all neighboring clocks are as close together as possible.
The gradient clock synchronization (GCS) problem seeks to synchronize clocks in a network so as to minimize the clock differences between neighboring nodes in the network. To make the problem concrete, consider the network whose nodes are villages. In each village, one or more churches has a clock, and the ringing of the church bells announces the local time to neighboring villages within earshot. The goal of the GCS problem is for each village to set its clock such that neighboring villages (those within earshot) agree on the time as closely as possible. Interestingly, while the the problem is local – only neighboring villages have to agree on the time – the best possible synchronization between neighboring nodes depends on the global size (or more specifically, the largest distance between villages) of the network. That is, the quality of synchronization between neighboring villages gets worse if we try to synchronize villages across all of Europe, as opposed to, say, Germany. This discovery is surprising, because the local ``view'' of a town within Germany is the same regardless of whether or not the rest of Europe is participating in the synchronization!
An optimal theoretical algorithm for the basic GCS problem has been known for 10 years, but there are still many open questions related to generalizing and implementing the algorithm. For example, recent work showed that the algorithm can be adapted to dynamic networks, where nodes and connections may be added and removed. Recently, our group also showed that the GCS algorithm can be generalized to fault-prone systems, where some of the nodes in the network behave adversarially.
In order to realize the power of the GCS algorithm in practice, our group is working to design hardware implementations of the GCS algorithm. That is, we seek to design physical circuits implementing the algorithm that are robust to the uncertainty inherent to digital circuits. Our group recently designed such an implementation for a system consisting of two processors sharing a single communication link. We are currently working to generalize the construction to arbitrary networks. Such an implementation will be applicable to designing high performance computers and computer networks.
Christoph Lenzen
DEPT. 1 Algorithms and Complexity
Phone +49 681 9325-1008
Email: clenzen@mpi-inf.mpg.de