Data Mining and Matrices
6 ECTS credits, summer semester 2015
Organization
Staff
Time & Location
- The lectures are on Tuesdays from 12:15 till 2 pm in room 029, building E1 5 (MPI-SWS) starting 21 April
- The tutorial groups meet on Wednesdays from 2 pm till 4 pm in room 022, building E1 4 (MPI-INF) starting 6 May
- Final exam: 28 July 12:00–14:00, Lecture Hall 001, building E1.3
Contact
News
- The grades from the course have been entered to HISPOS. Thank you for all who took this course!
Lecture slides
- 2015-04-21-introduction.pdf
- 2015-04-28-R-intro.pdf
- 2015-04-28-introToR.R
- 2015-05-05-lin_alg_and_svd.pdf
- 2015-05-12-pre-processing.pdf
- 2015-05-19-interpreting_and_computing_svd.pdf
- 2015-05-26-intro-to-nmf.pdf
- 2015-06-02-nmf_variations_and_applications.pdf
- 2015-06-09-cx_and_cur_decompositions.pdf
- 2015-06-16-ica_intro.pdf
- 2015-06-23-ica_algorithms.pdf
- 2015-06-30-spectral_methods.pdf
- 2015-07-07-bmf.pdf
- 2015-07-14-planted-patterns.pdf
- 2015-07-21-wrap-up.pdf
Sample solutions
The sample solutions to the homework assignments can be found here. You will need username and password to access them outside the university network; the credentials will be provided in the lectures.
Programming assignments
The programming assignments contain an assignment PDF and a zip file with data and necessary scripts. You need username and password to access the zip file outside the university network.
Information on exams
The final exam will be held on 28 July starting at 12:00 noon sharp. It will take place in lecture hall 001 of E1 3. More information about the final exam are on these slides.
Re-exam will be held in Thursday, 8 October, starting at 12:00 noon sharp in lecture hall 002 of building E1.3. If you want to take the re-exam, you must register via e-mail by 7 August twelve o'clock noon. The re-exam will cover the same contents as the actual exam with the addition of the last programming assignment.
If you need a certificate for the course, please contact the lecturer.
Course contents
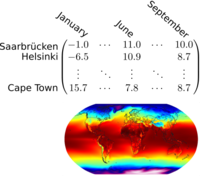
Temperature data can be seen as a matrix or as a map.
Graphs, relations, and sets of measurements over scalar variables form a significant part of the data types modern data analysis considers. All these different data types can be expressed as matrices, and matrix decomposition methods – originally developed for applications in linear algebra – are nowadays standard tools in any data analyst's toolbox.
The term ‘matrix decomposition’ covers a multitude of different techniques that are applicable to all stages of the knowledge discovery process, from pre-processing to visualization and analysis of the results. The main applications, nonetheless, are in data mining, where various decomposition methods are used to find regularities and patterns from a wide variety of data types.
In this course we will learn different matrix decomposition methods, including – but not limited to – Singular Value Decomposition, Principal Component Analysis, Non-Negative Matrix Factorization, and Independent Component Analysis. We will cover their strengths, their weaknesses, and their applications. The course intents to provide solid theoretical background to understand how and why the methods work, as well as hands-on experience on implementing and using the methods for real-world data analysis tasks.
To support its goals, the course consists of weekly lectures, fortnightly theoretical homework assignments, and three hands-on assignments.
Prerequisites
Good knowledge of basic linear algebra is required (at least Linear Algebra I or equivalent) as well as general mathematical skills on proving claims etc. Knowledge of either data mining or machine learning (e.g. either of core lectures on Information Retrieval and Data Mining or Machine Learning, or any of advanced courses on Convex Optimization, Topics in Algorithmic Data Analysis, or Elements of Statistical Learning) is also expected. The hands-on assignments are done using the R programming language, but no prior knowledge of R is required.
Information on assignments
The course has two types of assignments: theory-oriented fortnightly homework assignments and programming and problem-solving-oriented hands-on assignments. The homework sheets are handed out every second week and are due the next week (excluding the first homework sheet). Your earn a point for every homework question you provide a sufficiently detailed answer: the answer does not always need to be exactly correct, but correct answers without sufficient details are not valid. The homework sheets are discussed in the tutorial group day after their due date.
The hands-on assignments involve implementing methods discussed in the lectures and using the implementations for solving data analysis tasks. The solution to the hands-on assignments consists a written report and an appendix listing all the source code and R scripts required to duplicate the findings in the report. Every student must return their own solution to the assignments. Every second tutorial meeting covers the hands-on assignments: during these meetings, the students can obtain help for the current assignment and feedback from the previous assignments.
Grading and requirements for passing the course
The assignments can obtain failed, passed, or excellent grade. Every homework question is attributed one point if the solution is sufficiently complete.
To pass the course, the student must pass the final exam. To be allowed to take the final exam, the student must have received at least fifty per cent of the points given to the theoretical homework and passed all three hands-on assignments. At most one failed hands-on assignment can be upgraded to passing grade by doing extra homework.
Students can receive bonus points to improve their final grade. Every excellent hands-on assignment gives one bonus point, receiving at least 75 per cent of the homework points gives one bonus point, and receiving at least ninety per cent of the homework points gives one additional bonus point. For students who pass the final exam, every bonus point improves the final grade by one third, to a maximum of one full point (i.e. at most three bonus points will have an effect).
Suggested reading
- David Skillicorn: Understanding Complex Datasets: Data Mining with Matrix Decompositions. Chapman & Hall 2007
- Gene H. Golub & Charles F. Van Loan: Matrix Computations, 3rd ed. Johns Hopkins University Press 1996
- Jure Leskovec, Anand Rajaraman & Jeff Ullman: Mining of Massive Datasets, 2nd ed. Cambridge University Press 2015 (available online http://www.mmds.org)
